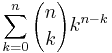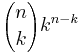Idempotence

Idempotence ( /ˌaɪdɨmˈpoʊtəns/ eye-dəm-poh-təns) is the property of certain operations in mathematics and computer science, that they can be applied multiple times without changing the result beyond the initial application. The concept of idempotence arises in a number of places in abstract algebra (in particular, in the theory of projectors and closure operators) and functional programming (in which it is connected to the property of referential transparency).

The term was introduced by Benjamin Peirce^[1] in the context of elements of an algebra that remain invariant when raised to a positive integer power, and literally means "(the quality of having) the same power", from idem + potence (same + power).

There are several meanings of idempotence, depending on what the concept is applied to:

A unary operation (or function) is idempotent if, whenever it is applied twice to any value, it gives the same result as if it were applied once. For example, the absolute value: abs(abs(x)) = abs(x).
A binary operation is idempotent if, whenever it is applied to two equal values, it gives that value as the result. For example, the operation giving the maximum value of two values is idempotent: max(x, x) = x.
Given a binary operation, an idempotent element (or simply an idempotent) for the operation is a value for which the operation, when given that value for both of its operands, gives the value as the result. For example, the number 1 is an idempotent of multiplication: 1 × 1 = 1.

1 Definitions
2 Common examples
3 Computer science meaning
- 3.1 Examples
4 See also
5 References

Definitions

Unary operation

A unary operation f, that is, a map from some set S into itself, is called idempotent if, for all x in S,

f(f(x)) = f(x).

In particular, the identity function id_S, defined by id_S(x) = x, is idempotent, as is the constant function K_c, where c is an element of S, defined by K_c(x) = c.

An important class of idempotent functions is given by projections in a vector space. An example of a projection is the function π_xy defined by π_xy(x, y, z) = (x, y, 0), which projects an arbitrary point in 3D space to a point on the x–y-plane, where the third coordinate (z) is equal to 0.

A unary operation f : S → S is idempotent if it maps all elements of S to fixed points. For a set with n elements there are

$\sum_{k=0}^n {n \choose k} k^{n-k}$

idempotent functions, where

${n \choose k} k^{n-k}$

is the number of idempotent functions with exactly k fixed points. The integer sequence of the number of idempotent functions as given by the sum above starts with 1, 1, 3, 10, 41, 196, 1057, 6322, 41393, ... (sequence A000248 in OEIS)

Binary operation

A binary operation ★ on a set S is called idempotent if, for all x in S,

x ★ x = x.

For example, the operations of set union and set intersection are both idempotent, as are logical conjunction and logical disjunction, and, in general, the meet and join operations of a lattice.

An element x of S is called idempotent for ★ if, for that element,

x ★ x = x.

In particular, an identity element of ★ is idempotent for the operation.

Connections

The connections between the three notions are as follows.

The statement that the binary operation ★ on a set S is idempotent, is equivalent to the statement that every element of S is idempotent for ★.

The defining property of unary idempotence, f(f(x)) = f(x) for x in the domain of f, can equivalently be rewritten as f ∘ f = f, using the binary operation of function composition denoted by ∘. Thus, the statement that f is an idempotent unary operation on S is equivalent to the statement that f is an idempotent element for the operation ∘ on functions from S to S.

Common examples

Functions

As mentioned above, the identity map and the constant maps are always idempotent maps. The absolute value function of a real or complex argument, and the floor function of a real argument are idempotent.

The function that assigns to every subset U of some topological space X the closure of U is idempotent on the power set of X. It is an example of a closure operator; all closure operators are idempotent functions.

The operation of subtracting the average of a list of numbers from every number in the list is idempotent. For example, consider the list 3, 6, 8, 8, 10. The average is 7. Subtracting 7 from every number in the list yields −4, −1, 1, 1, 3. The average of that list is 0. Subtracting 0 from every number in that list yields the same list.

Formal languages

The Kleene star and Kleene plus operators used to express repetition in formal languages are idempotent.

Idempotent ring elements

An idempotent element of a ring is, by definition, an element a that is idempotent with respect to the ring's multiplication.^[2] That is, a² = a.

A short list of important notions defined with idempotents includes:

A ring in which all elements are idempotent is called a Boolean ring. It can be shown that in every such ring, multiplication is commutative, and every element is its own additive inverse.
Two idempotents a and b are called orthogonal if ab = ba = 0. If a is idempotent in the ring R, then so is b = 1 − a; a and b are orthogonal.
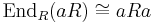If a is idempotent in the ring R, then aRa is again a ring, with multiplicative identity a. The ring aRa is often referred to as a corner ring of R. The corner ring arises naturally since the ring of endomorphisms $\mathrm{End}_R (aR)\cong aRa\,$ .
An idempotent a in R is called a central idempotent if ax = xa for all x in R. A ring in which all idempotents are central is called an Abelian ring. Such rings need not be commutative.
A trivial idempotent is one of the elements 0 and 1.
A primitive idempotent is an idempotent a such that aR is directly indecomposable.
A local idempotent is an idempotent a such that aRa is a local ring. This implies that aR is directly indecomposable, so local idempotents are also primitive.
A right irreducible idempotent is an idempotent a for which aR is a simple module. By Schur's lemma, End(aR) = aRa is a division ring, and hence is a local ring, so right (and left) irreducible idempotents are local.
A centrally primitive idempotent is a central idempotent a that cannot be written as the sum of two nonzero orthogonal central idempotents.
An idempotent e + I in the quotient ring R/I is said to lift modulo I if there is an idempotent f in R such that f + I = e + I.

Any non-trivial idempotent a is a zero divisor (because a(1 − a) = 0). This shows that integral domains and division rings don't have such idempotents. Local rings also don't have such idempotents, but for a different reason. The only idempotent contained in the Jacobson radical of a ring is 0. There is a catenoid of idempotents in the coquaternion ring.

Role in decompositions

The idempotents of R have an important connection to decompositon of R modules. If M is an R module and E=End_R(M) is its ring of endomorphisms, then A ⊕ B = M if and only if there is a unique idempotent e in E such that A = e(M) and B = (1 − e)(M). Clearly then, M is directly indecomposable if and only if 0 and 1 are the only idempotents in E.

In the case when M = R, End(R) = R, and so A⊕B = R as right modules if and only if there exists a unique idempotent e such that eR = A and (1 − e)R = B. Thus every module direct summand of R is generated by an idempotent. The ring R can be written as e₁R⊕ e₂R⊕...⊕e_nR with each e_i a local idempotent if and only if R is a semiperfect ring.

If a is a central idempotent, then the corner ring aRa = Ra is a ring with multiplicative identity a. Just as idempotents determine the direct decompositions of R as a module, the central idempotents of R determine the decompositions of R as a direct sum of rings. If R is the direct sum of the rings R₁,...,R_n, then the identity elements of the rings R_i are central idempotents in R, pairwise orthogonal, and their sum is 1. Conversely, given central idempotents a₁,...,a_n in R which are pairwise orthogonal and have sum 1, then R is the direct sum of the rings Ra₁,…,Ra_n. So in particular, every central idempotent a in R gives rise to a decomposition of R as a direct sum of the corner rings aRa and (1 − a)R(1 − a). As a result, a ring R is directly indecomposable as a ring if and only if the identity 1 is centrally primitive.

Working inductively, one can attempt to decompose 1 into a sum of centrally primitive elements. If 1 is centrally primitive, we are done. If not, it is a sum of central orthogonal idempotents, which in turn are primitive or sums of more central idempotents, and so on. The problem that may occur is that this may continue without end, producing an infinite family of central orthogonal idempotents. The condition "R does not contain infinite sets of central orthogonal idempotents" is a type of finiteness condition on the ring. It can be achieved in many ways, such as requiring the ring to be right Noetherian. If a decomposition R=c₁R⊕c₂R⊕...⊕c_nR exists with each c_i a centrally primitive idempotent, then R is a direct sum of the corner rings c_iRc_i, each of which is ring irreducible. (Lam 2001, p. 326)

Category of R modules

Lifting idempotents also has major consequences for the category of R modules. All idempotents lift modulo I if and only if every R direct summand of R/I has a projective cover as an R module. (Anderson 1992, p. 302) Idempotents always lift modulo nil ideals and rings for which R/I is I-adically complete.

Lifting is most important when I=J(R), the Jacobson radical of R. Yet another characterization of semiperfect rings is that they are semilocal rings whose idempotents lift modulo J(R). (Lam 2001, p. 336)

Lattice of ideals

One may define a partial order on the idempotents of a ring as follows: if a and b are idempotents, we write a ≤ b if and only if ab = ba = a. With respect to this order, 0 is the smallest and 1 the largest idempotent. For orthogonal idempotents a and b, a + b is also idempotent, and we have a ≤ a + b and b ≤ a + b. The atoms of this partial order are precisely the primitive idempotents. (Lam 2001, p. 323)

When the above partial order is restricted to the central idempotents of R, a lattice structure can be given. For two central idempotents e and f the complement ¬e = 1 − e and the join and meet are given by

e ∨ f = e + f − ef

and

e ∧ f = ef.

The ordering now becomes simply e≤f if and only if eR⊆fR, and the join and meet satisfy (e∨f)R=eR+fR and (e∧f)R=eR∩fR=(eR)(fR). It is shown in (Goodearl 1991, p. 99) that if R is von Neumann regular and right self-injective, then the lattice is a complete lattice.

Relation with involutions

If a is an idempotent, then 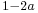$\scriptstyle 1-2a$ is an involution.

If b is an involution, then 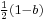$\scriptstyle\frac{1}{2}(1-b)$ is an idempotent, and these are inverse: thus if 2 is invertible in a ring, idempotents and involutions are equivalent.

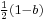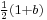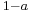Further, if b is an involution, then $\scriptstyle\frac{1}{2}(1-b)$ and $\scriptstyle\frac{1}{2}(1%2Bb)$ are orthogonal idempotents, corresponding to a and $\scriptstyle 1-a$ .

Numerical examples

One may consider the ring of integers mod n, where n is squarefree. By the Chinese Remainder Theorem, this ring factors into the direct product of rings of integers mod p. Now each of these factors is a field, so it is clear that the only idempotents will be 0 and 1. That is, each factor has 2 idempotents. So if there are m factors, there will be 2^m idempotents.

We can check this for the integers mod 6, R=Z/6Z. Since 6 has 2 factors (2 and 3) it should have 2² idempotents.

0 = 0² = 0³ = etc (mod 6)

1 = 1² = 1³ = etc (mod 6)

3 = 3² = 3³ = etc (mod 6)

4 = 4² = 4³ = etc (mod 6)

This also demonstrates the decomposition properties: because 3+4=1 (mod 6), there is a ring decomposition 3Z/6Z⊕4Z/6Z. In 3Z/6Z the identity is 3+6Z and in 4Z/6Z the identity is 4+6Z.

Other examples

Idempotent operations can be found in Boolean algebra as well.

In linear algebra, projections are idempotent. In fact, they are defined as idempotent linear maps. By choosing a basis, any projection gives an idempotent matrix.

An idempotent semiring is a semiring whose addition (not multiplication) is idempotent.

Computer science meaning

In computer science, the term idempotent is used more comprehensively to describe an operation that will produce the same results if executed once or multiple times. This may have a different meaning depending on the context in which it is applied. In the case of methods or subroutine calls with side effects, for instance, it means that the modified state remains the same after the first call. In functional programming, though, an idempotent function is one that preserves the property f(f(x)) = f(x).

This is a very useful property in many situations, as it means that an operation can be repeated or retried as often as necessary without causing unintended effects. With non-idempotent operations, the algorithm may have to keep track of whether the operation was already performed or not.

Stronger is nullipotent, meaning that the results are the same if executed zero or multiple times, which is synonymous with "no side effects".

Examples

Looking up some customer's name and address in a database are typically idempotent (in fact nullipotent), since this will not cause the database to change. Similarly, changing a customer's address is typically idempotent, because the final address will be the same no matter how many times it is submitted. However, placing an order for a car for the customer is typically not idempotent, since running the method/call several times will lead to several orders being placed. Canceling an order is idempotent, because the order remains canceled no matter how many requests are made.

A composition of idempotent methods or subroutines, however, is not necessarily idempotent if a later method in the sequence changes a value that an earlier method depends on – idempotence is not closed under composition. For example, suppose the initial value of a variable is 3 and there is a sequence that reads the variable, then changes it to 5, and then reads it again. Each step in the sequence is idempotent: both steps reading the variable have no side effects and changing a variable to 5 will always have the same effect no matter how many times it is executed. Nonetheless, executing the entire sequence once produces the output (3, 5), but executing it a second time produces the output (5, 5), so the sequence is not idempotent.^[3]

In the HyperText Transfer Protocol (HTTP), idempotence and safety are the major attributes that separate HTTP verbs. Of the major HTTP verbs, GET, PUT, and DELETE are idempotent (if implemented according to the standard), but POST is not.^[3] These verbs represent very abstract operations in computer science: GET retrieves a resource; PUT stores content at a resource; and DELETE eliminates a resource. As in the example above, reading data usually has no side effects, so it is idempotent (in fact nullipotent). Storing a given set of content is usually idempotent, as the final value stored remains the same after each execution. And deleting something is generally idempotent, as the end result is always the absence of the thing deleted.

In Event Stream Processing, idempotence refers to the ability of a system to produce the same outcome, even if an event or message is received more than once.

In a load-store architecture, instructions that might possibly cause a page fault are idempotent. So if a page fault occurs, the OS can load the page from disk and then simply re-execute the faulted instruction. In a processor where such instructions are not idempotent, dealing with page faults is much more complex.

The notion of idempotence at the end of a chain of operations was applied to so-called "desired-outcome" functions in the widely used configuration management software Cfengine in 1993, changing the industry approach to datacenter automation by bringing "self-healing" by simple repetition with a predictable outcome.

References

^ Polcino & Sehgal (2002), p. 127.
^ See Hazewinkel et. al. (2004), p. 2.
^ ^a ^b W3C, HyperText Transfer Protocol v. 1.1 Methods. See also HyperText Transfer Protocol.

Notes

“idempotent” at FOLDOC
Goodearl, K. R. (1991), von Neumann regular rings (2 ed.), Malabar, FL: Robert E. Krieger Publishing Co. Inc., pp. xviii+412, ISBN 0-89464-632-X, MR (93m:16006) 1150975 (93m:16006)
Hazewinkel, Michiel; Gubareni, Nadiya; Kirichenko, V. V. (2004), Algebras, rings and modules. Vol. 1, Mathematics and its Applications, 575, Dordrecht: Kluwer Academic Publishers, pp. xii+380, ISBN 1-4020-2690-0, MR (2006a:16001) 2106764 (2006a:16001)
Lam, T. Y. (2001), A first course in noncommutative rings, Graduate Texts in Mathematics, 131 (2 ed.), New York: Springer-Verlag, pp. xx+385, ISBN 0-387-95183-0, MR (2002c:16001) 1838439 (2002c:16001)
Lang, Serge (1993), Algebra (Third ed.), Reading, Mass.: Addison-Wesley Pub. Co., ISBN 978-0-201-55540-0 p. 443
Peirce, Benjamin.. Linear Associative Algebra 1870.
Polcino Milies, César; Sehgal, Sudarshan K. (2002), An introduction to group rings, Algebras and Applications, 1, Dordrecht: Kluwer Academic Publishers, pp. xii+371, ISBN 1-4020-0238-6, MR (2003b:16026) 1896125 (2003b:16026)